Time Constants Tutorial

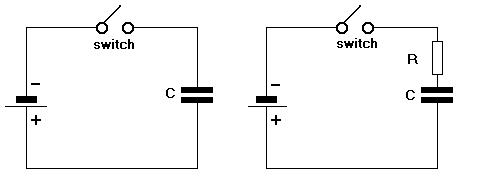
Similarly, the positive terminal attracts the negative electrons away from the lower plate. If the battery is now removed, C remains charged up to the battery voltage. This can be dangerous, since capacitors can remain charged to high voltages for a long time. If a screwdriver is now placed across the capacitor terminals, the surplus electrons on the upper plate will now flow to the lower plate.

The C is now discharged.

Doing this can also be dangerous.

The screwdriver has a low resistance, and Mr Ohm says "low resistance means high current". One vapourised screwdriver !!

Therefore large, highly charged capacitors must be discharged via a resistor, to limit the amount of discharge current that can flow.

In the second diagram, a resistor R has been placed in series with C. When the switch is closed, C charges from the battery, as described previously. The charging current passes through R. Since R limits the amount of current that can flow (Ohms law), C takes time to charge up to the battery voltage.

The larger the values of C and R, the longer C takes to charge. Liken it to filling a bucket with a hosepipe. The larger the bucket (C), and the more you stand on the hosepipe (R), then the longer it takes to fill the bucket. The value of C in Farads, multiplied by the value of R in ohms, gives us the TIME CONSTANT (RC), measured in seconds.

If C = 2 Farads and R = 10 ohms then RC = 20 seconds. This means that C will take 20 seconds to charge up to 63 % of the battery voltage. If it is a 100 volt battery, then after 20 seconds, the capacitor voltage will be 63 volts.

If we draw a graph of the increase of capacitor voltage against time, then we get a curve that is not linear ( not a straight line).

The curve is exponential. It increases rapidly at the start and then slows down. It gets slower and slower.

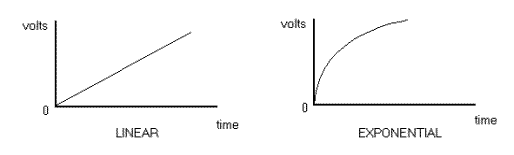
If C is discharged, by connecting a resistor across it, then the capacitor voltage falls BY 63 % after RC seconds.

Time constants are often used where a time delay is required.