|
Bels are a means of
comparing two powers or
two voltages.
For example, comparing
the power input to an
amplifier with the power
output as in the diagram
below.
The ratio of power in,
to power out, is the
power gain.
 In the next diagram, we
have three stages of
amplification.
To find the overall
power gain, we multiply
the individual gains.
10 X 6.5 X 9.2 = ?
Multiplying is not
friendly and also large
numbers can result.
 If we find the log of
the power ratio, the
answer is in Bels.
To do this, we work out
the power ratio and then
look up the log of this
value in log tables.
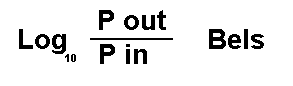
Since Bels are too big ,
we work in decibels (dBs)
as shown below.
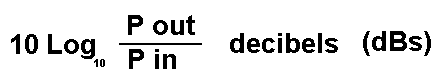 One advantage of
decibels are that the
numbers are usually more
convenient.
Below, the overall gain
is 1,000,000,000 or +90
dBs.
A gain of 1000 is +30
dB.
To find the overall
gain, individual gains
are added.
The + sign indicates a
gain.
A - sign would indicate
an attenuation.

If we are using voltage
ratios then use the
following formula.
 The ear has a
logarithmic response.
To make your amplifier
sound twice as loud you
must boost the power by
10 times. (+10 dB)
If you only double the
power (+3 dB), then you
will only just be able
to detect the increase
in volume.
Other points: there is
always a ratio, such as
the noise of Concorde
compared with the noise
of rustling leaves.
Sometimes there are
standard levels to be
compared with, such as 1
mW into 600 ohms for
audio, or 1 volt into 75
ohms for video.
10 dBm, for example, is
+10 dB relative to 1 mW.
It is not necessary to
do calculations, tables
are available, giving
the dB equivalent of
ratios, and vice-versa.
A useful table is shown
below.
 A gain of 400 watts is 2
x 2 x10 x 10 which is 3
dB + 3 dB + 10 dB + 10
dB = +26 dB.
A voltage gain of + 52
db = 20dB + 20 dB + 6 dB
+ 6 dB which is 10 x 10
x 2 x 2 = a gain of 400
times. |